| |
Semi-Transparent |
||||||
There have been a variety of attempts at making network programming fully transparent, some of which are ancestors of E (Actors, Concurrent Logic Programming, Concurrent Constraint Programming, Vulcan, Joule). Fully transparent means that any correct program written for a bunch of objects co-existing in a single addess space will remain correct when those objects are distributed over a network, and that any correct program written for a bunch of objects distributed over the network will remain correct when the objects in question are thrown together in the same address space. The computational model of the fully transparent systems must include only those feature that can be adequately supported in both contexts.
Carl Hewitt's seminal paper The Challenge of Open Systems explains the constraints of large scale mutually suspicious radically distributed systems. The Kahn and Miller Language Design and Open Systems explains what it means to design fully transparent programming languages that satisfy Hewitt's Open Systems constraints. All the E ancestors listed above satisfy the design principles listed in this paper. At ERights.org, when we refer to distributed computation, unless we state otherwise, assume we are talking about the radical distribution of Hewitt's Open Systems.
A Note on Distributed Computing argues, in effect, that the costs of these restrictions are too high for general purpose distributed computing. While we disagree with many of the particular arguments in the paper, we find the conclusions phrased much too strongly, and we find the above fully transparent systems much more plausible than this paper would suggest, nevertheless, E gives up on full transparency for the same reasons as what we take to be the main argument of the paper: There are compellingly useful features of local (single machine or single address space) computation that are not naturally available for distributed computation. It is too expensive to give up these features in the local case, where they are cheap; and for many of these, it is impossible or prohibitively expensive to support them in the distributed case. In order to support them in both cases, we must introduce a semantic non-uniformity between the two cases. (For a related but different case against full transparency, see Doug Lea's Design for Open Systems in Java.)
However, we can give up on full transparency without giving up all the benefits of transparency. We define semi-transparent network programming as the second half of the above definition: Any correct program written for a bunch of objects distributed over the network will remain correct when the objects in question are thrown together in the same address space. This definition implies that the semantics available in the distributed case are a subset of the semantics available locally. E is semi-transparent, and "vat" serves the role of "address space" in the above definition.
The most compelling cost difference between the intra-vat programming and distributed programming has to do with synchrony, latency, concurrency, atomicity, and reliability. Among objects in the same vat, the familiar synchronous sequential call-return programming, in which the caller waits for the callee to return, has the following attributes:
-
Synchrony makes efficient use of the CPU -- it can only do one thing at a time anyway
-
Adds little latency cost -- as both objects are about equally "close" to the CPU.
-
Enables cheap atomicity -- by disallowing other threads in the same address space (which is again cheap, as the CPU can only do one thing at a time anyway), and by disallowing synchronous communications between vats (which is also desireable on other grounds, as we'll see below).
-
Avoids partial failure handling -- a hardware failure cannot make some objects in an address space fail without making them all fail. The caller does not have to be prepared to react to the disappearance of the callee -- any disaster which kills the callee will kill caller as well, so it cannot react anyway. And vice versa.
-
Avoids temporal inconsistency -- Likewise, no hardware failure can sever the reference between caller and callee without killing them both. Therefore they are always in contact when they should be in contact, and can thereby safely make coordinated changes to their state.
By contrast, distributed inter-object invocation should be based on asynchronous one-way non-fully-reliable pipelined messages:
-
Asynchrony: The sender should send and continue, without waiting for a reply. This allows both processors to proceed in parallel. As is conventional in distributed systems analysis, time between vats must first be understood as a partial causal order, where the inter-vat messages are the causality links. The computation that happens is equivalent to any full order consistent with this partial order.
-
Latency: Pipes can be made wider but not shorter -- new technologies will give us ever more bandwidth, but they may never repeal the speed of light. Therefore, the need for network round trips should be kept to a minimum -- it must be reasonable to express distributed algorithms whose implementation requires no more round trips than reasonably necessary. E's promise-based promise pipelining allows computation to "use" the results of previous remote messages before these results have come back.
-
Mutual exclusion: While inter-machine mutual exclusion is very expensive (and under mutual suspicion, it's often prohibitively expensive), intra-vat mutual exclusion is free. Distributed computational patterns should make good use of this asymmetry, and our foundations should help us write such patterns.
-
Partial failure: Communication lines can temporarily go out, partitioning one part of the network from another. Machine can fail: in a transient fashion, rolling back to a previous stable state; or permanently, making the objects they host forever inaccessible. From a machine not able to reach a remote object, it is generally impossible to tell which of these failure scenarios is occurring. The system as a whole must smoothly continue in the face of these kinds of problems. It must be reasonably possible to write distributed apps whose surviving parts continue to provide valuable service while other parts are inaccessible. See Partial Failure Handling for more details.
- Temporal inconsistency: Once you write parts of an app to function in the face such inaccessibility of other parts, then these parts proceed forward and change state while out of contact. This conflicts with the strategy normally advocated by distributed systems designers for failure recovery: transparent masking of failure. You cannot simultaneously hide from the app the occurrence of failure while also allowing it to react to failure in order to continue functioning. E chooses failure-visibility. (By contrast, distributed databases typically choose failure-masking, which means their apps can get wedged during a partition.) The burden of choosing failure-visibility is that E must provide the programmer tools that can be used reliably at reasonable effort to recover distributed consistency on their own. Given the visibility of failure, such recovery is necessarily specific to the semantics of a given distributed app.
E handles this set of differences by adding surprisingly few new abstractions to the conventional set of single-addess space sequential pure object programming abstractions. In addition to the conventional NEAR reference, having all the synchrony and reliability properties available in a single address space, E introduces a reference taxonomy of other reference types including the EVENTUAL reference, which is the only kind that can span address spaces. In addition to the conventional message passing taxonomy of synchronous call-return control-flow constructs, which E only allows over conventional NEAR references, E's message passing taxonomy introduces the eventual send, which works over both NEAR and EVENTUAL references.
The properties of EVENTUAL references reflect the inescapable issues of distributed systems. However, the programmer doesn't need to know whether a reference is NEAR or EVENTUAL. In keeping with the principle of semi-transparency, when the programmer doesn't know, it is always correct to treat a reference as if it is EVENTUAL. You only need to know a reference is NEAR if you want to use some functionality available only on NEAR references -- like synchronous calling.
|
Known-NEAR
reference
|
Possibly-EVENTUAL
reference
|
|
|---|---|---|
|
Synchronous call-return: val := bob.msg(carol) |
Asynch one-way send: promise := bob <- msg(carol) |
|
|
Sequential programming
|
Event-loop programming
|
|
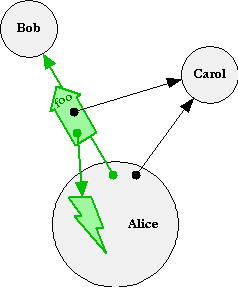
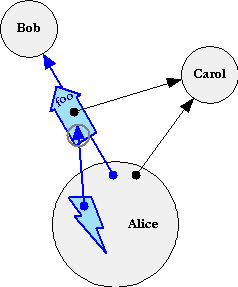
| Happens now | Happens eventually, and in order... | |
| Partition impossible | ...unless partitioned | |
|
control-flow outcome |
data-flow outcome |
At first, these last two picture may look identical but for the color change. But notice the reversal of the outcome arrow. As explained in Message Passing, the lightning bolt is the stack-frame in Alice in which she emitted a message to Bob. On the left, the arrow goes from the continuation part of the message to the stack-frame, implying that the stack-frame waits for a response to be sent to it along this arrow.
On the right, nothing points at the sending stack-frame, so it continues after emitting the message. Moreover, this stack-frame continues holding a promise for the outcome of the message -- the tail of the arrow -- even though the outcome itself hasn't been determined yet. The arrowhead with the gray halo is the ability to determine the resolution of the promise. It serves in the continuation-role of the message delivered to Bob. Messages sent on the arrowtail of a reference always move towards the arrowhead, even while the arrowhead is en-route. This is the basis for E's Promise Pipelining.
When Bob finishes reacting to a message, he reports an outcome to the message's continuation. On the left, Alice's stack-frame resumes by reacting to Bob's report. On the right, Bob's report resolves the promise that Alice holds -- the outcome of processing the message beomes the object designated by the reference.
Unless stated otherwise, all text on this page which is either unattributed or by Mark S. Miller is hereby placed in the public domain.
| |
|
report bug (including invalid html) |
||||||||