| |
Defining Objects |
||||||

This construct is used to define an object with multiple methods. This definition expression evaluates to an object, and the param variable is defined to hold this object. Each "to" with its following scope box is a method. No two methods may have the both the same verb and number of arg-patterns (or arity ). When this object is called, if the calling message does not have the same verb and arity as any of the object's methods, a java.lang.NoSuchMethodException is thrown.
If it does match a method, then the arguments are matched against the arg-patterns. If this match fails, a ***to be specified exception is thrown. It this succeeds, then, in the context of the resulting variable definitions, the method-expression is evaluated. The value of the method expression is the value of the call.
***Below is Really complicated explanation of shorthands, longhands, and I didn't get it
In this classic example, the outer object is written as a function, and the inner object is written out explicitly.
? pragma.syntax("0.8") ? def makePoint(x, y) :any { > def point { > to getX() :any {x} > to getY() :any {y} > } > } # value: <makePoint> ? def pt := makePoint(3, 5) # value: <point> ? pt.getX() # value: 3
Our original concise distance function is actually
? def distance {
> to run(x, y) :any {
> (x**2 + y**2).asFloat64().sqrt()
> }
> }
# value: <distance>
***must invent better examples than the predicate category thing. Need to start out with a simpler example, then in intro to this thing, you need concrete example of 2 predicates you want to use and make them conjunct, etc. Vector addition for points.***
Let's refer to a one argument function that returns a boolean as a predicate. In other words, let's say that an object with a one argument "run" method that returns a boolean is a predicate. We can think of a predicate as like a category -- whether the predicate's run method says true or false determines if the argument is or isn't in the category. However, when thinking of categories, it is natural to want to combine categories with the equivalent of intersection, union, etc.
The simple predicate notion does not provide for this, and if we required every predicate to support these new operations, we'd make it too hard to define a new predicate. Instead, here's makeCategory function, which, when given a predicate, gives back a category. Categories act like the predicate they wrap, but also support composition with the usual "&" (and),"|" (or), "^" (xor), and "!" (not) operators.
***no prior discussion of how & maps onto "and". I recommend using "and" in the example, and on the way thru, mention in passing we could have used "&" which maps onto "and".
? def makeCategory(pred) :any {
> def category {
> to (specimen) :any { pred(specimen) }
>
> to and(other) :any {
> makeCategory(def _(specimen) :any {
> pred(specimen) && other(specimen)
> })
> }
>
> # ... similarly for "or" and "xor"
>
> to not(other) :any {
> makeCategory(def _(specimen) :any {
> !(pred(specimen))
> })
> }
> }
> }
# value: <makeCategory>
Ok, now let's define some simple predicates and categories
? def evenPred(num) :any { num %% 2 == 0 }
# value: <evenPred>
? def even := makeCategory(evenPred)
# value: <category>
The even category was defined in two separate steps. Since a function definition expression has the function as its value, you can also define a category in one step:
? def small := makeCategory(def _(num) :any {
> num < 100
> })
# value: <category>
***having shown everyone this massive cuteness of the one line mega complex definition, ever after in examples use the 2 separate definition process***
Ok, let's intersect the categories.
? def both := even & small # value: <category> ? both(38) # value: true ? both(37) # value: false ? both(102) # value: false
Of these numbers, only 38 is both even and small.
Matching Messages
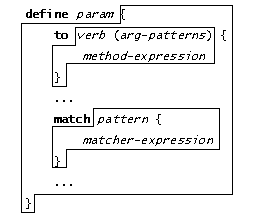
What if none of the methods match a call? Using the earlier form, an exception will always get throws back to the caller, but sometimes the callee would like to intervene. After the set of methods, an object definition may optionally have a sequence of matchers. These are the same matchers that appear in the switch statement, and you can validly think of them as if they were enclosed in a
if (.../*no methods match*/) { switch ([verb, args]) { match pattern { matcher-expression } ... } }
In other words, the verb and args from the incoming message are turned into a two-element ConstList which is then pattern matched against each of the patterns in sequence until a match succeeds. If none succeed, a ***to be specified exception is thrown. If one does match, the corresponding matcher-expression is evaluated, and the value of the matcher-expression is the value of the call.
One use of the flexibility is simply a more flexible alternative to method definition. Even though an individual method definition only accepts a fixed number of arguments, here's a version of our distance function that can accept any number of arguments.
? def distance { > match [=="run", args] { > var sum := 0.0 > for n in args { sum += n**2 } > sum.sqrt() > } > } # value: <distance> ? distance(3, 4) # value: 5.0 ? distance(3, 4, 5) # value: 7.0710678118654755
Although this example illustrates the power of matchers in object definitions, it's poor style. For such examples, its usually better to accept an EList as an argument.
***make sure in EList chapter you have an example of using an EList to send a variable size bag of arguments to a function
More interesting is the use of matchers for delegation. In the above makeCategory code, the category objects respond to "and", "or", "xor", and "not" themselves, but pass the "run(specimen)" message through to the wrapped predicate. If a predicate responds only to "run(specimen)", then a category that wraps this predicate is like the predicate and more. However, it a particular predicate object also responds to additional messages the category doesn't know about, the above category code will hide this part of the wrapped predicate.
Here is an alternative category implementation that uses match to delegate all messages it doesn't understand to the wrapped predicate.
? def makeCategory(pred) :any { > def category { > to and(other) :any { > makeCategory(def _(specimen) :any { > pred(specimen) && other(specimen) > }) > } > > # ... similarly for "or" and "xor" > > to not(other) :any { > makeCategory(def _(specimen) :any { > !(pred(specimen)) > }) > } > match [verb, args] { > E.call(pred, verb, args) > } > } > } # value: <makeCategory>
"E" is a primitive service which is always in scope. Use "E.call(pred,verb,args)" to call an object with a computed message, when you don't statically know the verb or the individual arguments. x.max(y) is equivalent to E.call(x,"max",[y]).
? def evenPred { > to (num) :any {num %% 2 == 0} > to foo() :any {"bar"} > } # value: <evenPred> ? def even := makeCategory(evenPred) # value: <category> ? even(3) # value: false ? even.foo() # value: "bar"
Even though the category code doesn't know anything about the "foo" message, the wrapping category, "even" delegated it to the wrapped predicate "evenPred".
Example: Lazy Evaluation
Here's a demonstration of a technique called lazy evaluation , where you have an object that represents the results of a potential calculation, but the calculation isn't performed until it's needed.
? var num := 0 # value: 0 ? def numThunk() :any { num } # value: <numThunk>
***need to define a thunk as an expression to evaluate, perhaps a primality test
The postponed argument given to LazyMaker is a no-argument function (ie, a thunk), and held by the resulting lazy object, represents the potential (or postponed) calculation. The actual calculation happens when the thunk is called. In lazy evaluation, once the calculation is performed, it's result is remembered and reused.
? def LazyMaker(postponed) :any { > var value := null > var hasValue := false > def lazy { > match [verb, args] { > if (hasValue) { > value > } else { > hasValue := true > value := postponed() > } > E.call(value, verb, args) > } > } > } # value: <LazyMaker>? def lazyNum := LazyMaker(numThunk) # value: <lazy> ? num += 1 # value: 1 ? lazyNum + 0 # value: 1
This addition causes numThunk to be evaluated, and the resulting value remembered.
? num += 1 # value: 2? lazyNum + 0 # value: 1
As we see, further changes to what numThunk would calculate no longer effect lazyNum.
Unless stated otherwise, all text on this page which is either unattributed or by Mark S. Miller is hereby placed in the public domain.
| |
|
report bug (including invalid html) |
||||||||