/ elib / capability / ode

From Functions To Objects

Object computation can be understood as the sum of three elements [Goldberg76] [Hewitt73]:

(footnote: The remaining feature often thought to be defining of object-oriented programming is inheritance. Though we do not view inheritance as as a fundamental ingredient of object computation, its widespread use in object-oriented programming practice motivates its inclusion in E. However, E's reconciliation of inheritance with capability security principles [Miller99] is beyond the scope of this paper.)

Lambda Abstraction

Lambda abstraction [Church41] is a pure theory of nested function definition and application. In E notation, conventional function definition and application should look familiar:

? pragma.syntax("0.8")

# E sample
def factorial(n) :any {
    if (n <= 0) {
        return 1
    } else {
        return n * factorial(n-1)
    }
}

? factorial(3)
# value: 6

The only unfamiliar element is the use of ":any" as a result guard declaration. The value returned is filtered through the optional result guard. Like a traditional type declaration, a guard determines what kind of values may pass through. The "any" guard allows any value to be returned, whereas the "void" guard always returns null. As we will see, E also allows optional guard declarations on variable definitions.

Nested function definition, familiar from all lexical lambda languages including ALGOL60, Scheme, and ML, should also look familiar:

# E sample
def makeAddr(x) :any {
    def adder(y) :any {
        return x + y
    }
    return adder
}

? def addThree := makeAddr(3)
# value: <adder>

? addThree(5)
# value: 8

The call to makeAddr returns a closure -- effectively a version of the adder function that adds 3 to its argument. Church originally thought about this as substitution -- return an adder function in which x has been replaced by 3. Unfortunately, this simple perspective generalizes poorly. An alternative perspective is to consider a function, such as that held in the addThree variable, to be a combination of a behavior -- the static code for adder, and state -- the runtime bindings for its free variables. x in adder is a free variable in that adder uses x, but the corresponding definition of x is inherited from adder's creating context. In the remainder of this paper, we will refer to such free state variables as instance variables.

Such functions already have the most often cited attribute of objects: they are a combination of encapsulated state together with behavior that has exclusive access to that state. Ignoring for a moment the message-name "foo", the Granovetter Diagram describes an important aspect of the lambda calculus. Imagine that Alice, Bob, and Carol are three functions. If, in the initial conditions, Alice contains a binding for Bob and Carol, then Alice's behavior can give Bob access to Carol.

def ... {                    # enclosing context
    def bob := ...           # instance variable bob somehow bound to Bob
    def carol := ...         # instance variable carol somehow bound to Carol
    def alice(...) :void {   # defines Alice
        bob(..., carol, ...) # Alice sends Bob a reference to Carol
    }
    ...
}

Adding Message Dispatch

The most visible difference between a function and an object is that a function's behavior is written to satisfy just one kind of request, and all calls on that function are forms of that one request. By contrast, an object's behavior enables it to satisfy a variety of different requests (each with a separate method). A request to an object (a message) identifies which of these requests is being made. There is nothing fundamental here; objects have been trivially built from functions, and vice-versa, many times in the history of computer science. In E, behaviors-as-bundles-of-methods and requests-as-messages are the more primitive notions, of which functions are a degenerate case.

# E sample
def makePoint(x,y) :any {
    def point {
        to __printOn(out) :void { out.print(`<$x,$y>`) }
        to getX()          :any { return x }
        to getY()          :any { return y }
        to add(other)      :any {
            return makePoint(x + other.getX(), y + other.getY())
        }
    }
    return point
}

? def p := makePoint(3,5)
# value: <3,5>

? p.getX()
# value: 3

? p + makePoint(4,8)
# value: <7,13>

From a lambda-calculus perspective, makePoint is like makeAddr -- it is a lexically enclosing function that defines the variable bindings used by the object it both defines and returns. From an object perspective, makePoint is simultaneously like a class and constructor -- both defining the instance variables for points, and creating, initializing, and returning individual points. We have found such lambda-based object definition to be simpler, more expressive, and more intuitive, than either of the common choices -- class-based and prototype-based object definition. The lambda-based technique for defining objects dates back at least to 1973 [Hewitt73], so we find it distressing that the other two are often assumed to be the only available choices.

The returned points are clearly object-like rather than function-like. Each point's behavior contains four methods -- __printOn, getX, getY, and add -- and every request to a point starts by naming which of these services is being requested. Now we see that the "foo" in the Granovetter Diagram is simply a message-name. Extending our earlier example, Alice's behavior would be:

        bob.foo(..., carol, ...)

Some shortcuts above need a brief explanation.

• "a + b" is merely syntactic shorthand for "a.add(b)", and similarly for other expression operators.

• The command line interpreter prints a value by sending it the __printOn message.

• The string between back-quotes and containing $-prefixed expressions is a quasi-string. Like interpolated strings in Perl, it evaluates to a string by evaluating the nested expressions and printing them into the enclosing string.

• Finally, functions are simply one-method objects where the method is named "run". The previous makeAddr is therefor just syntactic shorthand for:

def makeAddr {
    to run(x) :any {
        def adder {
            to run(y) :any {
                return x.add(y)
            }
        }
        return adder
    }
}

Adding Side Effects

Two features of object programming implied by the Granovetter Diagram have been left out of computation as so far described.

• First, the diagram implies that Bob is obtaining access to Carol, but computation as so far described gives Bob no means for holding on to this access.

• Second, we understand the diagram to say that Alice is giving Bob access to Carol herself, not a copy of Carol [Deutsch99]. However, in computation as has been described so far, Carol is indistinguishable from a copy of Carol. We cannot distinguish between pass-by-reference-sharing and pass-by-copy, but the Granovetter Diagram clearly intends to show specifically pass-by-reference-sharing. Were computation adequately described purely in terms of pass-by-copy, the Granovetter Diagram would be unnecessary.

The introduction of side effects solves both of these problems.

Starting with lambda calculus (or with lambda plus message dispatch), there are many ways to add side effects. The approach used by E, Scheme, ML and many other lambda languages is to introduce assignment. In E, variables are non-assignable (or "final") by default. For a variable to be assignable, it must be declared with "var".

How does assignment make Carol potentially distinct from a duplicate of Carol? Consider:

# E sample
def makeCounter(var count) :any {
    def counter {
        to incr() :any { return count += 1 }
    }
    return counter
}

? def carol := makeCounter(0)
# value: <counter>

? carol.incr()
# value: 1

Two otherwise identical counters are distinct because they have distinct count variables that increment separately. All those who have access to the same counter are able to see the side effects of incr messages sent by others who have access to this same counter.

How does assignment enable Bob to retain access he has been given to Carol? By assigning an incoming message-argument to an instance variable:

def makeBob() :any {
    var carol := null
    def bob {
        to foo(..., newCarol, ...) ... {
            carol := newCarol
        }
        ...
    }
    return bob
}

Composites & Facets

Technically, by introducing assignment, we have made each assignable variable into a distinct primitive variable-object, referred to as a Slot. A user-defined object then contains bindings from the names of these variables to these Slots. The Slots in turn contain the bindings to the current values of the variables. When the programmer writes a use-occurrence of the variable in an expression, this causes the containing object to send a getValue() message to the Slot to get its current value. When the programmer writes an assignment, this causes the containing object to send a setValue(newValue) message to the Slot.

When a variable is only in the scope of one object, as in all the above examples, we usually ignore this distinction, and speak as if the containing object has bindings directly from the variable names to the current values of these variables. But this shortcut does not work for code such as:

# E sample
def makeCounterPair(var count) :any {
    def upCounter {
        to incr() :any { return count += 1 }
    }
    def downCounter {
        to decr() :any { return count -= 1 }
    }
    return [upCounter, downCounter]
}

? def [i, d] := makeCounterPair(3)
# value: [<upCounter>, <downCounter>]

? i.incr()
# value: 4

? i.incr()
# value: 5

? d.incr()
# problem: <NoSuchMethodException: <a downCounter>.incr/0>

? d.decr()
# value: 4

Each time makeCounterPair is called, it defines a new count variable and returns a list of two objects, one that will increment and return the value of this variable and one that will decrement and return it. This is a trivial example of a useful technique -- defining several objects in the same scope, each providing different operations for manipulating a common state held in that scope.

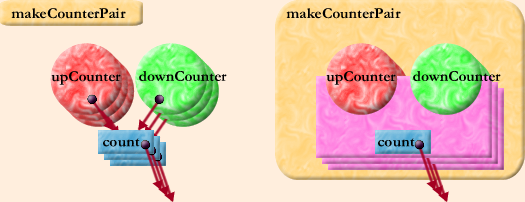
On the left we see, diagrammed in explicit detail, the objects and relationships resulting from each call to makeCounterPair. The stacking represents that a new triple is created by each call. None of these objects actually refer to makeCounterPair, so there's no arrow to it. On the right, each triple is visualized as a single composite. This view also shows that makeCounterPair is in scope during the definition of each composite, and so they might reference it.

Like an individual object, a composite is a combination of state and behavior. Like an individual object, the state consists of all of the variables within the composite. The behavior consists of all of the code within the composite, but here we have an important difference.

The behavior elicited by a message to the composite depends not just on the message, but, obviously, on which object of the composite receives the message. Objects on the surface of the composite -- objects which may be referred to from outside the composite, like upCounter and downCounter -- are facets of the composite. The variable-object, count, need not be considered a facet since we can tell that no reference to it can escape from the composite.

The aggregation of a network of objects into a composite is purely subjective -- it allows us to hide detail when we wish. The technique works because the possible interactions among composites obey the same rules as the possible interactions among individual objects -- these rules are therefor compositional.

The Dynamic Reference Graph

When speaking of object computation, all too much emphasis is often placed on the objects themselves. The fabric of an object system is the dynamic reference graph. As suggested by the Granovetter Diagram, objects (or composites) are the nodes of this graph and references are the arcs. Only computation within the graph brings about changes to the topology of the graph (the who refers to whom relationships), and it only brings about those changes that are enabled by the graph's current topology. To learn the perspective of the Granovetter Diagram is to see the dynamic reference graph as primary, and objects themselves as secondary [Kay99].