/ elib / capability / ode

Overview: Capability-based Financial Instruments

Presented at Financial Cryptography 2000

Mark S. Miller, ERights.org
Chip Morningstar, Communities.com
Bill Frantz, Communities.com

Abstract

Every novel cooperative arrangement of mutually suspicious parties interacting electronically -- every smart contract -- effectively requires a new cryptographic protocol. However, if every new contract requires new cryptographic protocol design, our dreams of cryptographically enabled electronic commerce would be unreachable. Cryptographic protocol design is too hard and expensive, given our unlimited need for new contracts.

Just as the digital logic gate abstraction allows digital circuit designers to create large analog circuits without doing analog circuit design, we present cryptographic capabilities as an abstraction allowing a similar economy of engineering effort in creating smart contracts. We explain the E system, which embodies these principles, and show a covered-call-option as a smart contract written in a simple security formalism independent of cryptography, but automatically implemented as a cryptographic protocol coordinating five mutually suspicious parties.

Introduction

From simple abstractions, great power may bloom. Sometimes, this power comes not from wholly new ideas, but rather from the emergent insights that arise when bits of common wisdom from disjoint communities come together. For example, Shannon's formalization of the notion of information [Shannon48] built a bridge between the electrical engineer's intuitions about signals, encodings, and noise, and the mechanical engineer's intuitions about temperature and thermodynamic efficiency.

This paper takes a first step in unifying the work of the object programming community, the capability-based secure operating systems community, and the financial cryptography community. Historically:

• objects have been strong on abstraction and composition,

• operating systems have been strong on providing a shared platform in which disparate processes can interact without being able to damage one another, even if they contain malicious code, and

• financial cryptography has been strong on cooperative protocols allowing mutually suspicious parties to trade a diversity of rights in the absence of a mutually-trusted platform.

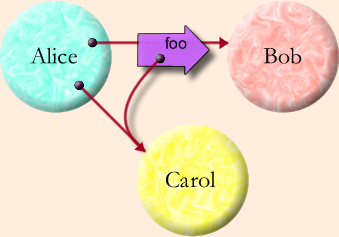
Unfortunately, each has been weak in the areas where the other two are strong. By bridging the intuitions of these communities, we can engineer systems with the strengths of all three. The bridge described in this paper is based on a joint appreciation, across all three communities, of a common abstraction, illustrated by the Granovetter Diagram shown on the right. The sociologist Mark Granovetter originally developed diagrams of this type to illustrate how the topology of interpersonal relationships changes over time, as people introduce people they know to each other [Granovetter73]. Though Granovetter devised this diagram in the context of human relations, we have found it to be a powerful notation for understanding the relations between computational objects in a network.

We present this abstraction from six perspectives:

1. As the basic step of Object Computation.
2. As the foundation for Capability Security.
3. As a Cryptographic Protocol implementing distributed capabilities.
4. As a Public Key Infrastructure, where certificates act like messages, transmitting authorization among the players.
5. As the core Game-Rule for secure computation modeled as a vast multi-player game.
6. As material from which to build a diversity of Financial Bearer Instruments.

We are building the E system [E] to unify these perspectives. E is a simple, secure, distributed, pure-object, persistent programming language. E blends the lambda calculus, capability security, and modern cryptography. In integrating these diverse features, E brings the diverse virtues of the Granovetter Operator to life. Throughout the paper we present our examples in E, explaining the language briefly as needed.

Since we can only touch upon each perspective briefly within the space allowed for this paper, we have chosen breadth over depth, so that even a brief treatment can unify the perspectives. Hopefully our references and future writings will provide the needed depth as well.

Six Perspectives

1. Objects. Most importantly, the Granovetter Diagram shows the computation step fundamental to all object computation: the "message send" (in Smalltalk terminology) or the "virtual member function call" (in C++ terminology). Alice, Bob, and Carol are three objects. In the initial conditions, Alice holds a reference to (points at, has access to) Bob and Carol. Dynamically, we see that Alice is sending a foo message to (calling the foo member function of) Bob, in which a parameter of the message (call) is a copy of Alice's reference (pointer, access) to Carol. For conciseness, we will refer to this computation step as the Granovetter Operator.

   Object-oriented message passing, along with encapsulation and polymorphism, enables modular programming. By designing the interfaces between modules on a need-to-know basis, we satisfy the principle of information hiding [Parnas72] that is the basis of much important software engineering theory and practice.

   Read more...

2. Capability Security. The Granovetter Operator becomes a security primitive given the following constraint: If Bob does not already have a reference to Carol, Bob can only come to have a reference to Carol if a third party, such as Alice,

   • already has a reference to Carol, and
   • already has a reference to Bob, and
   • voluntarily decides to share with Bob her reference to Carol.

   Adding this property to an object system transforms it into a capability system. In a capability system, only connectivity begets connectivity. In a capability system, an object's authority to affect the world outside itself is determined solely by what references it holds, since the only way the object can cause an external effect is to send a message via one of these references. Consequently, the mechanics of reference-passing determine how authority can change over time.

   The capability model prohibits certain possibilities, such as forgeable references or mutable global variables, that the object computation model allows (though it does not require them either). Although, in principle, the object computation model is perfectly compatible with these prohibitions, most embodiments of object computation (typically in the form of programming languages) disregard the boundaries imposed by the capability model [Kahn88]. We explain why E does stay within these boundaries, and so is capability-secure (as are these systems [Hewitt73, Tribble95, Rees96]). We will present an implementation of capability-based money as an example.

   The main capability-system design rule, the principle of least authority (sometimes called the "principle of least privilege" [Saltzer75]) requires one to design interfaces such that authority is handed out only on a need-to-do basis [Crockford97].

   Read more...

3. Cryptographic Protocol. Imagine now that Alice, Bob, and Carol are objects residing on three separate machines on a computer network. Distributed object systems, such as CORBA [CORBA] and RMI [Wollrath99], provide for the diagrammed message send to proceed over the network, while preserving the core semantics of the object computation model. However, these are cooperative protocols, in that they rely on the assumption that the machines involved are correctly cooperating. By contrast, a cryptographic protocol implementing the Granovetter Operator must also preserve the semantics of the capability model, including the prohibitions, in the presence of mutually suspicious objects residing on mutually suspicious machines.

   We briefly explain Pluribus, E's cryptographic capability protocol, turning E into a securely distributed language. We examine how the money example (from the previous section) transparently distributes by showing how Pluribus automatically maps the pieces of the example to stock cryptographic-protocol elements.

   Read more...

4. Public Key Infrastructure. Some PKIs, like SPKI (the Simple Public Key Infrastructure [Ellison99]), interpret digital certificates primarily as statements authorizing the players to perform various actions on various resources. In the Granovetter Diagram, the message arrow foo can be seen as such a certificate, signed by Alice, stating that Bob has the authority to perform the action represented by Carol. This certificate is meaningful if and only if there is a similar certificate granting Alice this right, and so on, back to the creator/owner of Carol. Should Bob choose to exercise this authority, he would present the certificate-chain (or its logical equivalent) as proof that he has received this authorization.

   The enforceable subset of SPKI can be seen as an off-line, auditable, heavyweight, non-confinable, semi-capability system, as opposed to E's on-line, repudiatable-by-default, lightweight, confinable, full-capability system. Perhaps, by comparing these, we may figure out how to build systems with some of the best of both.

   Read more...

5. Game Rules. During a player's turn in a board game, the state of the board constrains what moves that player may make. From these possible moves, the player chooses a particular move, which changes the board and thereby alters the moves then available to the other players. Recall the three conditions needed for Bob to receive a reference to Carol from Alice. The first two conditions are constraints on the possible moves available to Alice (and so correspond to mandatory security). The third condition is that Alice must choose to make this move (and so corresponds to discretionary security). If Alice actually does choose to make this move, she thereby changes the moves available to Bob -- afterwards Bob may both send messages to Carol and send messages to yet other parties introducing Carol to them, whereas previously he could not.

   Attempts to formalize the semantics of computation, including secure computation, have failed to capture the core intuitions of computer security practitioners. Fundamental to these intuitions is the notion of mutually suspicious, separately interested agents, interacting within a framework of rules, under constraints of partial knowledge, each in order to pursue their own interests. The formal tools for capturing such intuitions are to be found in non-zero-sum, partial-information game theory [Schelling63]. The Granovetter Diagram expresses the core game-rule governing secure capability-based distributed multi-agent computation, viewed as a vast multi-player game.

   We have yet to exploit this perspective in order to apply game theory to computation in this manner, but we hope this explanation may point the way. We do not explore the game perspective further in this paper.

   Read more...

6. Financial Bearer Instruments. If Carol provides a useful service, then the ability to send messages to Carol may be a useful right. Perhaps Carol answers questions from a store of knowledge that she alone is privy to. Perhaps she can affect some aspect of the external world, such as pixels on a display or the cash dispenser of an automated teller machine. Any secure system of electronic rights must solve at least three problems:

   • How to represent who currently has what rights.
   • How to enable rights holders to exercise those rights they have, and no more.
   • How to enable rights holders to securely transfer these rights.

   The static reference relationships among objects exactly represent who currently has what rights. Since a right is exercised by sending a message to an object that embodies the right, such as Carol, the rule that you can send a message to any object you have a reference to, but no others, provides for the exercise of those rights you have, and no others. Finally, the transition shown on the Granovetter Diagram is both the secure transfer to Bob of the right to pass messages to Carol, as well as the exercise, by Alice, of whatever right Bob may represent.

   In the face of widespread misuse of the term "electronic commerce", we should remember that "commerce" entails more than just the ability of a merchant to accept monetary payment. Commerce is a rich set of market interactions that emerge when territory and abilities are abstracted into "rights", and a rich set of arrangements that emerge for the mutually acceptable transfer of these rights. For large scale electronic commerce, we should concern ourselves with those rights which are both representable electronically and enforceable electronically, and with mutually-enforceable arrangements for their transfer.

   The Granovetter Diagram by itself shows the simplest -- in the electronic world -- interesting such electronic right: a non-exclusive, specific, exercisable, non-assayable bearer instrument. By contrast, the money example from sections 2 and 3 shows an exclusive, fungible, non-exercisable, assayable bearer instrument. We sketch a taxonomy of other enforceable electronic rights, and show how most of these can be built by simple compositions of the Granovetter Operator. Derivative rights, including derivative financial instruments, are composed from underlying rights via familiar object abstraction. We show a covered call option as an example.

   Read more...